answer 3:4 - Relationship between K and total protein concentration
Ligand binding obeys the law of mass action:
Kd = [P] [X]free / [PX]
In the above equation I emphasize the fact that the law of mass action applies to the equilibrium concentration of free ligand, which is to be distinguished by the total ligand: [X]free = [X]tot - [PX].
If the total protein concentration is low with respect to the ligand concentration one has [X]free ≅ [X]tot. This is the ideal condition for studying ligand binding equilibria.
Unfortunately selecting the ideal conditions, i.e. [P]tot < < [X]tot and [X]free ≅ [X]tot is not a decision of the researcher, but the consequence of a series of practical constraints:
1) the ligand concentrations to be used are defined by the Kd because significant changes in ligand saturation occurs over a ligand concentration range spaced between Kd/10 and 10 Kd; it is very convenient to reason in terms of a logarithmic space of ligand concentrations centered on log(Kd).
2) the protein concentration is defined by the sensitivity of the instrument used to detect [P] and [PX]. For example if P and PX differ because of their absorbance, [P]tot is defined by the differential extinction coefficients of P and PX and is usually in the high micromolar range; if fluorescence is used one gains a factor of 100 or more on sensitivity and [P]tot may be as low as the high nanomolar range.
High affinity does not refer, per se, to specific values of Kd; rather a high affinity ligand is one whose Kd is high with respect to the protein concentration required to measure ligation. If we select more sensible instruments to measure ligation, we convert a high affinity ligand into a non-problematic ligand; unfortunately this is not always possible and we depend on the nature of the signal that monitors ligation.
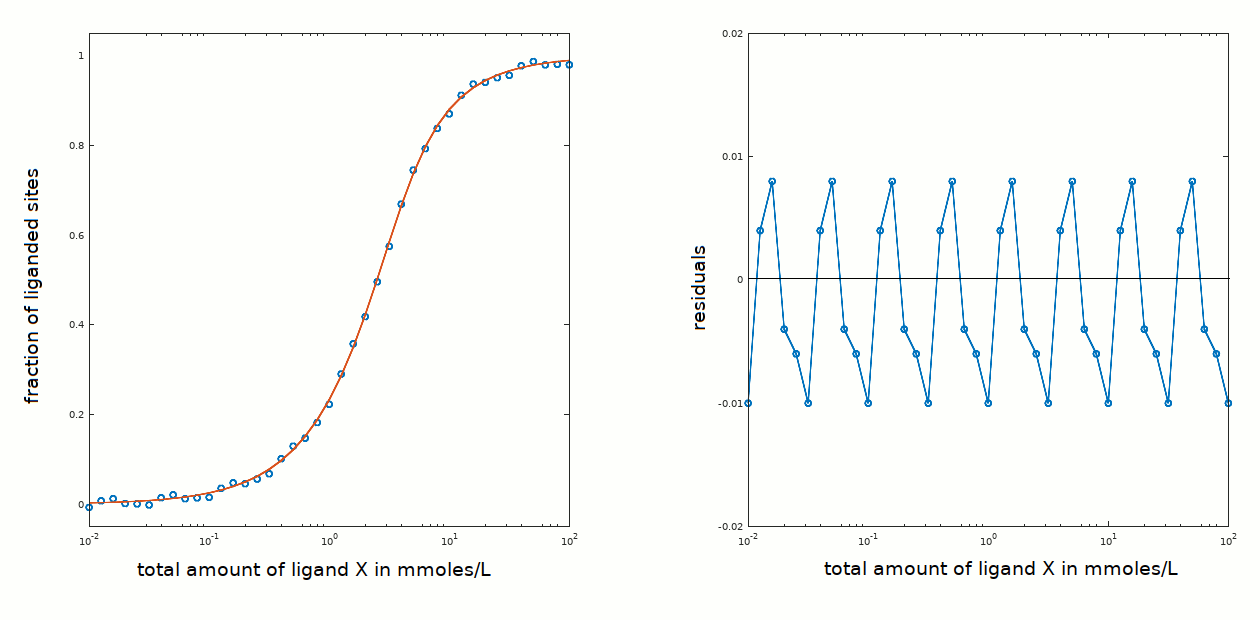
In the present example ligand binding is centered around a total ligand concentration of approx. 2 mM that is low with respect to the protein concentration used (3 mM); thus the approximations [P]tot < < [X]tot and [X]free ≅ [X]tot are not applicable.
We rewrite the law of mass action as follows:
It is interesting to compare the concentrations of Xtot and Xfree (with [X]free = [X]tot - [PX]):
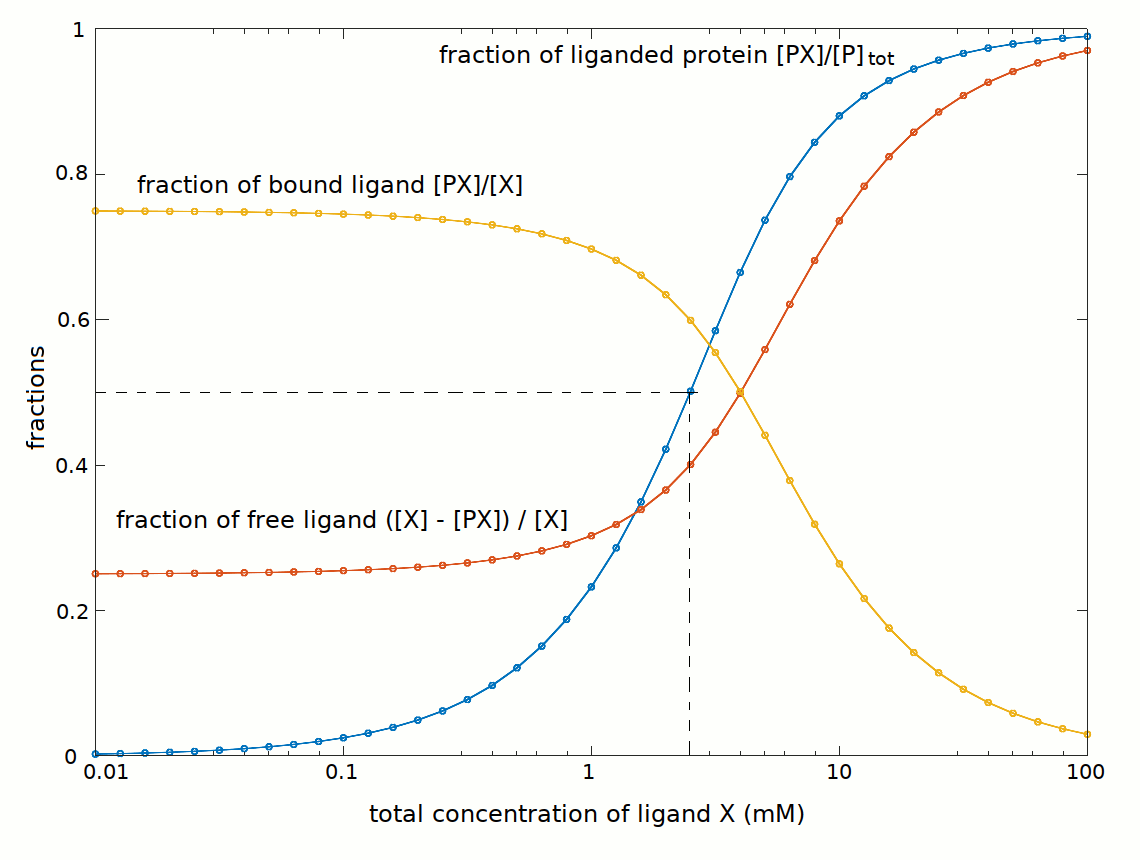
At the total ligand concentration required to saturate half the available binding sites we have the following conditions:
[X]tot = 2.5 mM
[PX] = [P] = [P]tot / 2 = 1.5 mM
[X]free = Kd = C50 = [X]tot - [PX] = 1 mM
It is important to state that the C50 is the free ligand concentration required to saturate half the available binding sites, and is a function of Kd; it is not the total ligand concentration required to saturate half the available binding sites.
How do we recognize the problem of a high affinity ligand and avoid confusing it wityh the case of positive cooperativity? The crucial test is that ligation occurs over a range of ligand concentrations that includes [P]tot; in the present example binding occurred over a ligand concentration range centered around 2.4 mM (see this page) and the protein concentration was 3 mM.
This tutorial is complete. Back to table of content