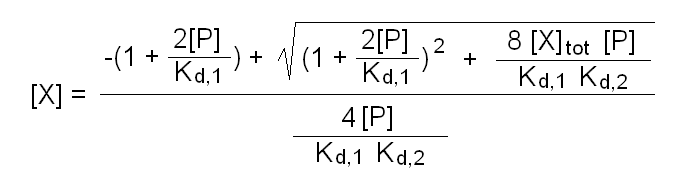LIGAND BINDING: INVERTING THE ROLES OF LIGAND AND TARGET Andrea Bellelli Department of Biochemical Sciences “A. Rossi Fanelli”, Sapienza University of Rome, Italy A lecture not yet given.       ABSTRACT       In a typical binding experiment, the concentration of one of the reaction partners is kept constant, while that of the other is systematically increased to monitor the formation of the complex. The reactant whose concentration is constant is called the target, that whose concentration is varied is called the ligand. The choice of which partner is the target and which one is the ligand is dictated by practical convenience: it is usually preferable that the target is the partner that provides the signal, and that the ligand is a monomer in solution. In this lecture I shall demonstrate that when both the target and the ligand are monomeric, inverting the respective roles has no effect on the recorded binding isotherm, whereas when the reaction stoichiometry is different from 1:1 inverting the roles of the reactants does affect the binding isotherm one can record.       Selected references by the author       Bellelli A and Carey J. (2018) Reversible Ligand Binding, Wiley.       1. LIGAND BINDING REACTION WITH 1:1 STOICHIOMETRY       A binding reaction with 1:1 stoichiometry obeys the following laws: P + X <==> PX Kd = [P][X] / [PX] The roles of the protein (P) and the low molecular weight ligand (X) in these equations are identical, thus if [P] is kept constant while [X] is varied one obtains a hyperbolic binding isotherm identical to the one obtained at constant [P] and variable [X]. In this case the only considerations that decide which reactant it is convenient to vary are those of convenience: (i) it is convenient to keep constant the concentration of the reactant that provides the signal (e.g. if one records the reaction between myoglobin and oxygen by absorbance spectroscopy, it is convenient to keep constant the concentration of myoglobin, because it yields the absorbance signal whereas oxygen does not contribute); and (ii) it is convenient to keep constant the concentration of the reactant which is more difficult to obtain at high concentration (usually the protein).       2. LIGAND BINDING REACTION WITH HIGHER THAN 1:1 STOICHIOMETRY       Usually reaction stoichiometries different than 1:1 are due to the protein having more binding sites for the ligand. E.g. for homodimer: P + 2 X <==> PX + X <==> PX2 If the protein is non-cooperative and the binding sites are identical (e.g. a the proetin is a non-cooperative homodimer), the system behaves as in the case of 1:1 stoichiometry and inverting the roles of target and ligand does not change the shape of the ligand biding isotherm. If the signal distinguishes the two species PX and PX2 one may realize that the distribution of the liganded species differs between the two cases (i.e. if P is the target PX is preferentially populated at low concentrations of X and PX2 is preferentially populated at high concentrations of X).       If the protein is cooperative, The ligand binding isotherm recorded at constant concentration of P, and variable X, is completely different from the one obtained at constant concentration of X, and variable P.       We define: Kd,1 = [P][X] / [PX] Kd,2 = [PX][X] / [PX2] Taking into account the statistical factors, we write: [P] or [X] = reference species [PX] = [P] 2[X]/Kd,1 [PX2] = [P] [X]2/Kd,1Kd,2       These replationships do not depend on P being target and X being ligand or vice versa.       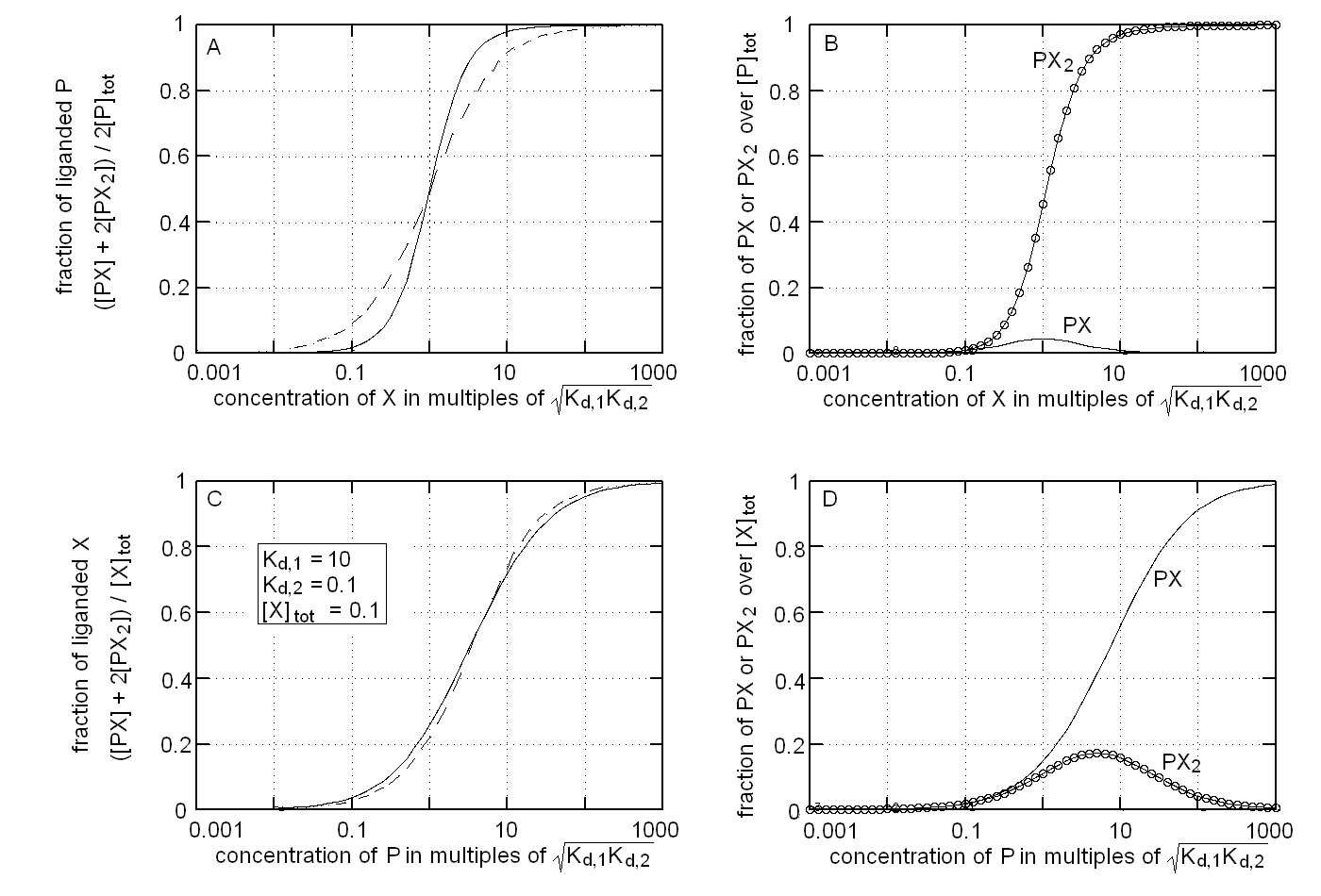If the experiment is carried out at constant concentration of P (=target) and variable concentration of X (=ligand) one has: [P]tot = [P] (1 + 2[X]/Kd,1 + [X]2/Kd,1Kd,2) Fraction of liganded sites = ([X]/Kd,1 + [X]2/Kd,1Kd,2) / [P]tot The binding isotherm and population of ligation intermediates for this experimental condition are reported in Fig.1, panels A and B respectively. We remark that: (i) the binding isotherm simulated with Kd,1 > > Kd,2 is steeper than that for a single site protein wth the same overall affinity for the ligand (dashed line), i.e. it displays positive cooperativity (Fig. 1A); (ii) the intermediate PX is poorly populated and attains its maximum population at relatively low values of [X], being completely replaced by PX2 at high valeus of [X] (Fig. 1B).       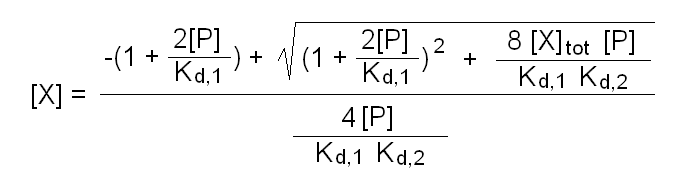If the experiment is carried out at constant concentration of X (=target) and variable concentration of P (=ligand) one has: [X]tot = [X] (1 + 2[P]/Kd,1 + 2[X] [P]/Kd,1Kd,2) The above binding polynomial yields the 2nd degree equation: 2[X][P]/Kd,1Kd,2 + [X](1 + 2[P]/Kd,1) - [X]tot = 0 whose solution yields [X]: Fraction of bound ligand = 2[P][X]/Kd,1 (1 + [X]/Kd,2) / [X]tot The binding isotherm and population of ligation intermediates for this experimental condition are reported in Fig.1, panels C and D respectively. We remark that: (i) the binding isotherm simulated with Kd,1 > > Kd,2 is broader than that for a single site protein wth the same overall affinity for the ligand (dashed line), i.e. it displays negative cooperativity (Fig. 1C); (ii) the intermediate PX2 is poorly populated and attains its maximum population at relatively low values of [X], being completely replaced by PX at high valeus of [X] (Fig. 1D). These considerations are the exact opposite of those I gave for panels A and B, i.e. in this case inverting the roles of ligand and target drastically changes the shape of the ligand binding isotherm and the distribution of ligation intermediates.             Home page