1) La cooperativita' nel legame dei ligandi e' una conseguenza di interazioni omotropiche positive o negative; implica sempre che la proteina sia un oligomero costituito da piu' subunita' tra loro uguali o almeno simili. Si noti che mentre non tutti gli oligomeri presentano cooperativita', nessuna monomerica puo' presentare questa proprieta'.
Cooperativita' positivaimplica che la prima molecola di ligando e' legata con affinita' minore dell'ultima; la sigmoide del grafico che descrive la frazione di saturazione in funzione del logaritmo della concentrazione del ligando libero e' piu' ripida di quella di una proteina non cooperativa. Cooperativita' negativa implica le proprieta' esattamente inverse: la prima molecola di ligando e' legata con affinita' maggiore dell'ultima e la sigmoide di legame e' meno ripida di quella di una proteina non cooperativa:
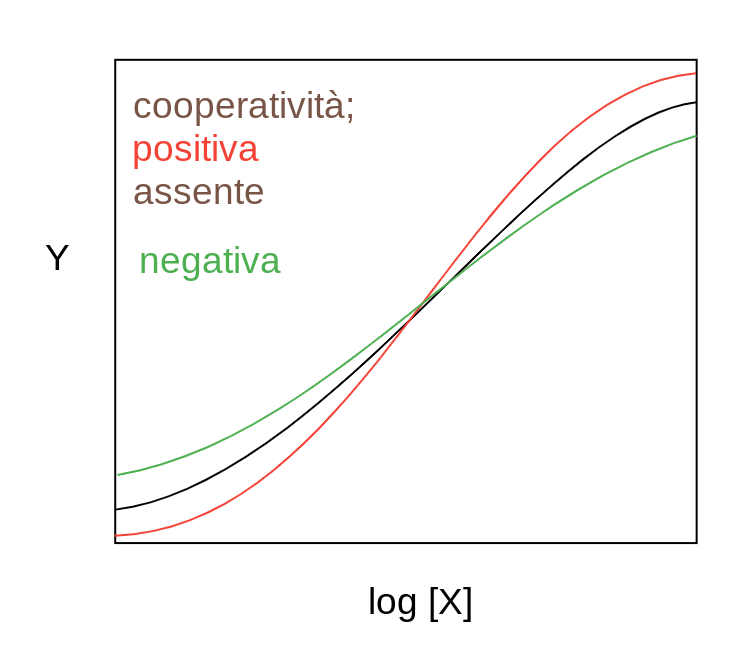
2) Sia la cooperativita' positiva che quella negativa possono avere grande rilievo per la fisiologia: la cooperativita' positiva aumenta l'efficacia di un trasportatore e rende un enzima piu' capace di rispondere a variazioni di concentrazione del suo substrato; in una via metabolica tende a mantenere costante la concentrazione degli intermedi. La cooperativita' negativa in un enzima mantiene costante la velocita' di formazione del prodotto nonostante possibili variazioni di concentrazione del substrato; in una via metabolica mantiene costante in flusso di metaboliti. Come regola generale l'enzima che si trova all'inizio di una via metabolica presenta cooperativita' positiva mentre quelli che catalizzano le reazioni successive possono presentare cooperativita' negativa.
3) La cooperativita' sembra violare la legge di azione delle masse e la sua spiegazione matematica richiede un modello complesso. I modelli matematici che spiegano la cooperativita' appartengono essenzialmente a due famiglie: i modelli seuqenziali e i modelli concertati.
4) Il modello sequenziale e' storicamente il piu' antico e fu proposto originariamente da L. Pauling nel 1935; ebbe varie riformulazioni e varianti (Wyman; Koshland; etc.). Il concetto cruciale e' il seguente: il legame della prima molecola di ligando induce una variazione conformazionale a livello terziario (ligand-induced fit) e questo causa la formazione di una interazione con le subunita' vicine. La seconda molecola di ligando si lega ad una subunita' che riceve l'interazione della subunita' legata, che ne cambia la conformazione; l'affinita' e' di conseguenza modificata (aumentata o diminuita). Il modello di Pauling implica che le specie parzialmente legate col ligando della proteina cooperativa siano asimmetriche, anche quando le specie completamente legata e completamente non legata sono simmetriche. Un armadio scorrevole a due ante ci da una rappresentazione macroscopica dell'asimmetria, per un dispositivo che presenta cooperativita' negativa (i siti di legame possono essere: entrambi chiusi; entrambi semichiusi; uno chiuso e uno aperto; ma non possono essere entrambi aperti):
 |  |
Ad esempio in una molecola che ha quattro subunita' identiche, tutte capaci di interagire tra loro (schema "tetraedrico" di Pauling) la reazione risulta:
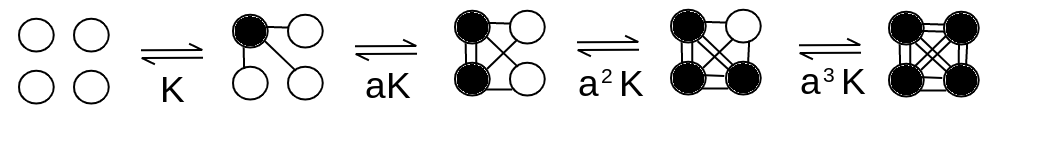
La concentrazione degli intermedi di reazione risulta:
[P]: specie di riferimento
[PX] = [P] 4[X]/K
[PX2] = [PX] 3[X]/2aK = [P] 6[X]2/aK2
[PX3] = [PX2] 2[X]/3a2K = [P] 4[X]3/a3K3
[PX4] = [PX3] [X]/4a3K = [P] [X]4/a6K4
Questo porta al seguente polinomio di legame:
Nota bene: i coefficienti numerici che precedono la [X] sono i coefficienti statistici; tengono conto del fatto che esistono 1 sola forma di P, 4 possibili forme di PX (diverse per la posizione dell'unica molecola di ligando nel tetramero), 6 possibili forme di PX2, 4 possibili forme di PX3 e 1 sola forma di PX4. In pratica la possibile distribuzione del ligando all'interno del tetramero e' binomiale e i coefficienti sono quelli caratteristici della potenza di un binomio.
Linus Pauling riassunse il concetto di base del suo modello (per l'emoglobina; il ligando considerato era l'ossigeno) in termini estremamente chiari, che vale la pena di riportare testualmente: "RT ln K' is the free energy change accompanying the addition of oxygen to heme and RT ln (a) is the additional free energy stabilizing two interacting HbO2; that is the free energy is decreased by RT ln (a) for each interaction ..." [L. Pauling The oxygen equilibrium of hemoglobin and its structural interpretation].
5) Il modello concertato o allosterico fu proposto originariamente da Monod, Wyman e Changeux nel 1965. Ipotizza che la molecola allosterica possa assumere due configurazioni quaternarie chiamate T e R e caratterizzate da diversa affinita' per il ligando. Le due configurazioni strutturali non sono cooperative; cioe' T lega il ligando con affinita' definita dalla costante di equilibrio KT (e R con KR). Le due configurazioni quaternarie sono simmetriche: tutte le subunità devono essere nella stessa configurazione strutturale; la simmetria implica cooperativita' positiva. Un modello macroscopico della simmetria puo' essere realizzato accoppiando due pinze per i manici; le configurazioni possibili per il sistema sono simmetriche (entrambe chiuse o entrambe aperte):

L'equilibrio tra le due configurazioni quaternarie e' governato dalla costante allosterica L. Lo schema di reazione e' il seguente (le reazioni indicate in rosso sono quelle statisticamente piu' rilevanti):
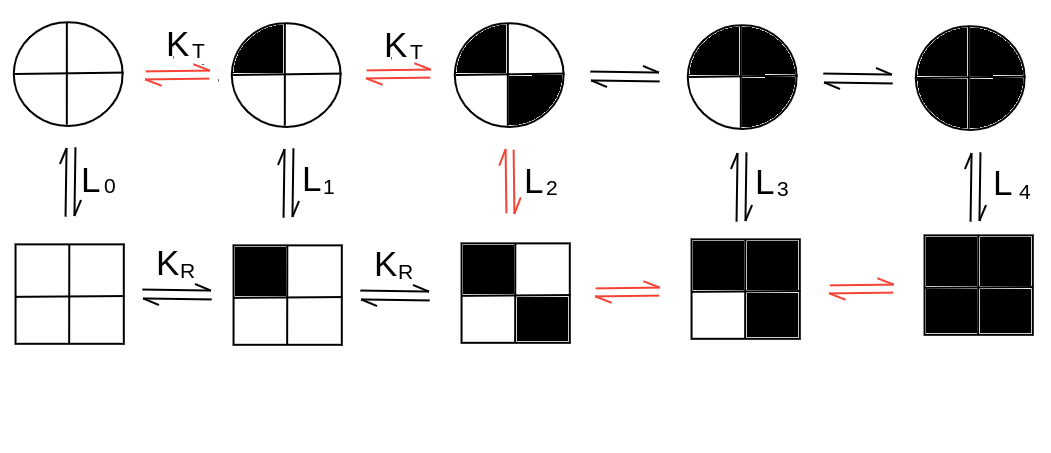
RPX --> RP --> TP ; il prodotto delle costanti risulta KR L0
RPX --> TPX --> TP ; il prodotto delle costanti risulta L1 KT
Poiche' le due vie chiudono un quadrato termodinamico abbiamo che: L1 KT = L0 KR
Da cui deriviamo: L1 = L0 KR / KT
Le costanti KR e KT sono definite nel senso della dissociazione; pertanto avendo la specie R maggiore affinita' della T per il ligando avremo KR < KT e L1 < L0.
Generalizzando: Ln = L0 (KR / KT)n
La dipendenza di L dal numero di ligandi legati e' cruciale per il meccanismo della cooperativita'. Cosideriamo ad esempio il caso dell'emoglobina umana che in condizioni fisiologiche presenta i seguenti parametri funzionali per l'ossigeno (a 20oC): KR=0.2 mmHg; KT=40 mmHg; c=KR/KT=0.005; L0=105. Con questi parametri possiamo calcolare L4=L0 c4=6.25x10-5. Ovvero: il primo ligando si combina con una proteina che e' per il 99.999% nello stato T; il quarto ligando con una che e' per il 99,994% nello stato R e questo rende ragione della differenza di affinita' tra la prima e la quarta reazione.
Il polinomio di legame in questo modello risulta dalla somma di due polinomi separati, uno per la forma R e uno per la forma T; per specie di riferimento si prende la proteina non legata nella forma R, e si scala il polinomio della forma T per il fattore L0:
6) Rappresentazione termodinamica dei modelli sequenziale e concertato
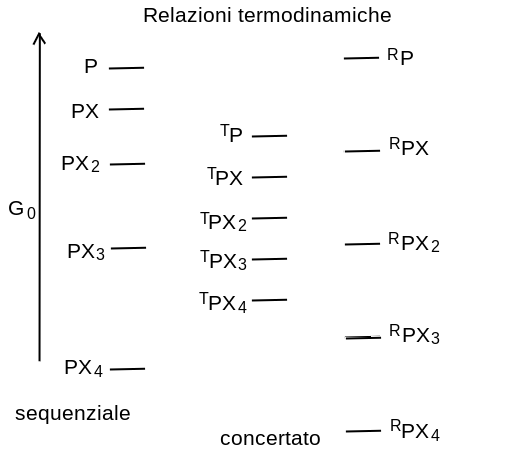
La differenza cruciale tra lo schema di reazione sequenziale e quello concertato sta nel fatto che nel primo il ligando causa il cambiamento conformazionale (terziario), nel secondo il ligando seleziona la conformazione pre-esistente per la quale ha la maggiore affinita'; nelle parole di J.P. Changeux: "This is, to my opinion, the birth date of the "two-state mechanism" of pre-existing conformational states (R <--> T) and, by consequence, of a "selective" rather than an "instructive" effect of the ligands." [J.P. Changeux The Origins of Allostery: From Personal Memories to Material for the Future].
7) Identical linkage in una proteina allosterica e' relativamente semplice. Se i due ligandi hanno lo stesso effetto nel modificare Ln, la proteina rimarra' costantemente legata e nello stato R e la partizione tra i due ligandi risultera' non cooperativa; se invece i due ligandi non hanno lo stesso effetto su Ln la partizione risultera' cooperativa.
8) Heterotropic linkage in una proteina allosterica e' molto frequente e di grande importanza in biologia: consente ai sistemi biologici di regolare la loro funzionalita' in risposta a stimoli (variazione di concentrazione di effettori) interni o esterni. Nella formulazione originale del modello di Monod, Wyman e Changeux l'effettore non modifica KR e KT ma ha affinita' diversa per le due conformazioni; di conseguenza modifica L0 secondo una legge simile a quella osservata per l'interazione omotropica. La stechiometria di legame puo' essere qualsiasi: da una molecola di effettore per subunita' ad una molecola per oligomero. Per una proteina che presenta un solo sito di legame per oligomero:
In questa equazione TKY rappresenta la costante di dissociazione dell'effettore Y dalla proteina nel suo stato T e RKY quella per lo stato R. Se TKY < RKY lo stato T ha maggiore affiinita' per l'effettore Y dello stato R e L0' > L0 (l'effettore preferisce lo stato T e quindi aumenta il valore della costante L; regolazione eterotropica negativa); e viceversa (regolazione eterotropica positiva). L'equazione ha due casi limite:
a) l'effettore lega in misura significativa una sola delle due configurazioni quaternarie; ad esempio T. L'equazione si riduce a: L0' = L0 (1 + [Y] / TKY)
b) l'effettore lega entrambe le configurazioni quaternarie, con diversa affinita', ed e' presente in concentrazione molto superiore alle costanti TKY e RKY; l'equazione si riduce a: L0' = L0 RKY / TKY
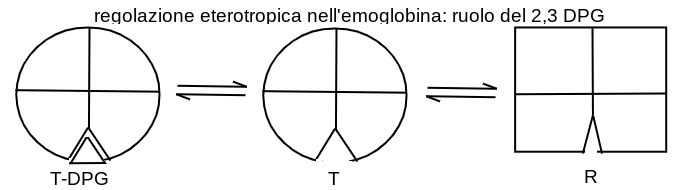
Esempi di regolazione eterotropica negativa sono dati dal legame del 2,3 bis-fosfo glicerato (2,3 DPG) all'emoglobina o dal legame del fosfo-enol piruvato alla fosfofruttochinasi. Il 2,3 DPG si combina con l'emoglobina in un sito di legame che si trova all'interfaccia tra le due subunita' β ed ha maggiore affinita' per lo stato T che per lo stato R, nel quale il sito di legame si restringe. Pertanto il 2,3 DPG favorisce lo stato T (aumenta il valore della costante allosterica L) e riduce l'affinita' dell'emoglobina per l'ossigeno.
| Meccanismo di reazione concertato (allosterico) | Meccanismo di reazione sequenziale | |
| simmetria (tutte le subunita' assumono la stessa struttura terziaria) | obbligata | vietata (almeno in alcuni intermedi di legame e' richiesta l'asimmetria) |
| cambiamento strutturale quaternario | necessario | non necessario |
| cooperativita' omotropica | solo positiva | possibile sia positiva che negativa |
| effetto del ligando | selezione della specie proteica con maggiore affinita' | il ligando causa il cambiamento conformazionale terziario |
| regolazione eterotropica | quasi sempre presente, sia positiva che negativa | possibile ma non frequentee |
| ruolo metabolico (per gli enzimi) | di solito nelle primissime reazioni di ogni ciclo | indifferente; spesso la cooperativita' negativa e' presente negli enzimi che catalizzano le reazioni intermedie e finali dei cicli |