|
Experiments, theories and problems Andrea Bellelli Department of Biochemical Sciences “A. Rossi Fanelli”, Sapienza University of Rome, Italy A lecture given on Tuesday July 1st, 2014 in Nove Hrady (CR), at the FEBS Avanced Course "Ligand Binding Theory and Practice" organized by Jannette Carey, Rudiger Ettrich and Wei-Feng Xue. 
Abstract Cooperative ligand binding is a fundamental function of a large number of proteins, whose physiological relevance spans from transport, catalysis and regulation of the cell cycle. The reversible oxygen combination to hemoglobin is a prototype of cooperativity and has been convincingly demonstrated to be a consequence of allostery, the ability of the protein to adopt either of (at least) two structural and energy states. The simplest theoretical framework that correlates cooperativity and allostery is the two-state model originally proposed by Monod, Wyman and Changeux (MWC) in 1965, whose critical assumption is that of perfect structural symmetry. Crucial questions on the structure-function (i.e. on the allostery-cooperativity) relationship in hemoglobin have been thoroughly addressed in the past with reference to the MWC model and provide quite a consistent picture, whose key elements will be reviewed in the lecture. These are: (i) the quaternary constraint, and its structural bases; (ii) the demonstration of two quaternary structures, to be correlated with two energy states, irrespective of ligation; (iii) the relationship between structure, oxygen affinity and dissociation of the tetrameric molecule into dimers; (iv) the structural and functional characterization of ligation intermediates; (v) the direct demonstration of the equilibrium between allosteric conformations, by means of rapid kinetic techniques. Open questions on the details of the structure-function relationship in hemoglobin remain, and suggest that the MWC model needs extensive refinements: e.g. it provides an unsatisfactory description of allosteric effects, and is not consistent with the experimentally determined time course of oxygen dissociation; moreover metastable allosteric conformations have been observed that seem to violate the symmetry principle. Some of these findings may be reconciled with the model advocating some form of energy degeneracy within the low affinity allosteric conformation, but others would require major changes on which no agreement has been found yet. Selected references by the author Bellelli A, Brunori M, Miele AE, Panetta G, Vallone B. (2006) The allosteric properties of hemoglobin: insights from natural and site directed mutants. Curr. Protein Pept. Sci. 7: 17-45 (reprinted and updated in 2013) Bellelli A. (2010) Hemoglobin and Cooperativity: Experiments and Theories. Curr. Protein Pept. Sci. 11: 2-36. Bellelli A. and Brunori M. (2011) Hemoglobin allostery: variations on the theme. Biochim. Biophys. Acta (Bioenergetics), 1807, 1262-1272. Hemoglobin as a model system Hemoglobin reversibly binds oxygen. Several experimental methods may be used to study this reaction, e.g.: 1) we can measure free and bound O2 by manometric techniques. This method requires high protein cncentration and is destructive (i.e. requires large amounts of protein, and is time consuming). 2) We can measure free oxygen by manometric or potentiometric methods (or total oxygen by volumetric methods) and the fractional oxygen saturation of Hb by absorption spectroscopy. Equivalence of spectroscopic and manometric measurements of hemoglobin oxygen saturation was demonstrated by Anderson and Antonini (J. Biol. Chem. 1968; 243: 2918-20). Some of the features that contribute to make Hb a model system are: 1) it is abundant and easy to purify; it can be studied by manometric methods that were available early (chemistry was born in the XVIII century from the study of gases). 2) It contains 0.335% of iron: this easily lead to the determination of its minimum molecular weight of 16700 (by Zinoffski in 1885). 3) The stoichiometry of oxygen binding could also be determined early at 1.34 mL/g (by Huffner in 1884). This lead to the correct estimate of the stoichiometry of the reaction at a Fe:O2 ratio of 1:1. 4) Its oxygen binding properties are astonishingly complex (i.e. interesting). More than a century ago, Christian Bohr discovered that Hb binds O2 cooperatively, i.e. its affinity for the gas increases with its fractional saturation. In 1913 Archibald Vivian Hill (who in 1922 received the Nobel prize for Physiology and Medicine), recognized that cooperativity would only be possible in a macromolecule having more than a single oxygen binding site, and proposed a mechanism that assumed n sites: Hb + n O2 <==> Hb(O2)n K = [Hb(O2)n] / ([Hb] [O2]n) [Hb(O2)n] / ([Hb] = K [O2]n and log [Y / (1-Y)] = log (K) + n log ([O2] with Y = fractional O2 saturation = [Hb(O2)n] / ([Hb(O2)n] + [Hb]) The Hill coefficient, estimated as the slope of the Hill plot usually assumes non-integer values in the range 2.5 - 3, that Hill interpreted as estimates of the average degree of polymerization of Hb in solution (i.e. he expected that Hb was a mixture of dimers with MW 32,000, trimers with MW 48,000 and possibly higher order polymers). As explicitly remarked by Hill, cooperativity implies that the ligation intermediates (e.g. Hb polimers containing only ne molecule of bound O2) are less populated than one would expect for a non-cooperative system, and indeed his model implied that ligation intermediates are absent altogether and that partially oxygenated hemoglobin is a mixture of unliganded species (Hb) and fully oxygenated ones (Hb(O2)n). Remark: in the absence of cooperativity the distribution of intermediates should follow the binomial statistical distribution: 1 = (Y + (1-Y))n: i.e. the fraction of fully liganded species should be Yn ... Hill's theory is nowadays obsolete. Suffice it to say that the Hill plot of Hb presents two n=1 asymptotes, not anticipated by Hill. Nevertheless, the Hill coefficient n is still used as an empirical measure of cooperativity and indicates the minimum number of interacting sites. 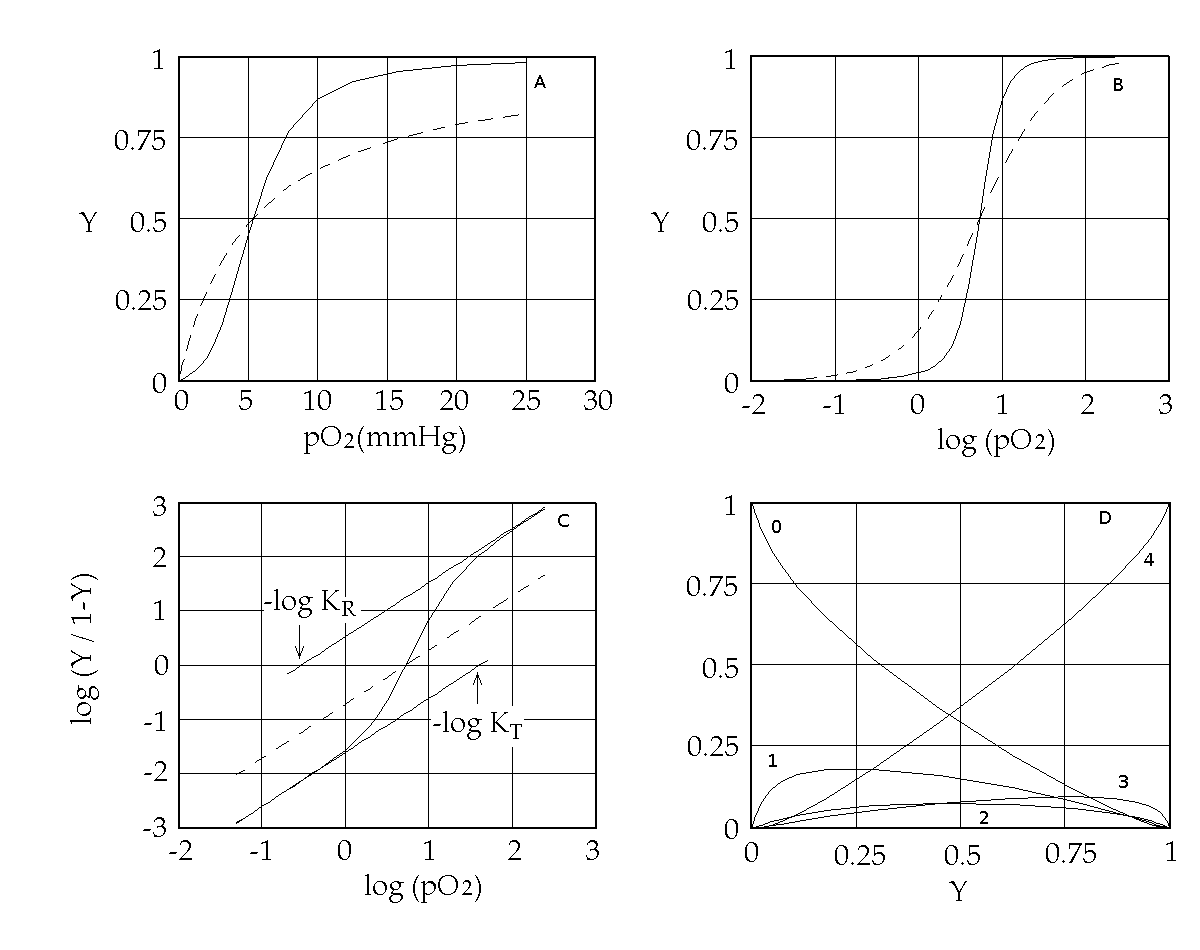
Figure 1. Representations of the oxygen binding isotherm of HbA (continuous lines, as calculated from the data of K. Imai, 1983). The behaviour of a non cooperative O2 carrier with the same overall affinity is reported for comparison (dashed lines) Panel A: the Y vs. pO2 plot. Panel B: the Y vs. log (pO2) plot. An interestng characteristic of this plot is that log (pO2) is proportional to the free energy associated with changes in concentration. Panel C: the Hill plot. Panel D: the population of ligation intermediates, taking into account that, contrary to Hill's hypotheses, Hb is a stable tetramer. In 1925 Gilbert S. Adair demonstrated (by osmometry) that Hb is a stable tetramer in solution, with MW = 64,000. Comparison with previous data lead immediately to the conclusion that each macromolecule can bind 4 molecules of O2. Adair also proposed a chemical scheme that implied 4 equilibrium constant, that could explain cooperativity if the fourth constant is greater that the first (i.e. if the first molecule of O2 is bound less strongly than the fourth). However, four equilibrium constants are not the minimum requirement for explaining cooeprativity and indeed it is sufficient that Hb has access to two constants (i.e. to two thermodynamic states, corresponding to the asymptotes of the Hill plot). At least two states The two asymptotes of the Hill plot clearly point to a minimum number of two thermodynamic states of Hb. But what do we mean withthe term "state"? If we recall that the equilibrium constant is associated to a free energy change by the relation: ΔG0 = - RT ln K , it follows that an oxygen carrier that occupies one single thermodynamic state has a single equilibrium constant (identified by a single n=1 line in the Hill plot), a single ΔG0, with the energy profile depicted in Fig.2. 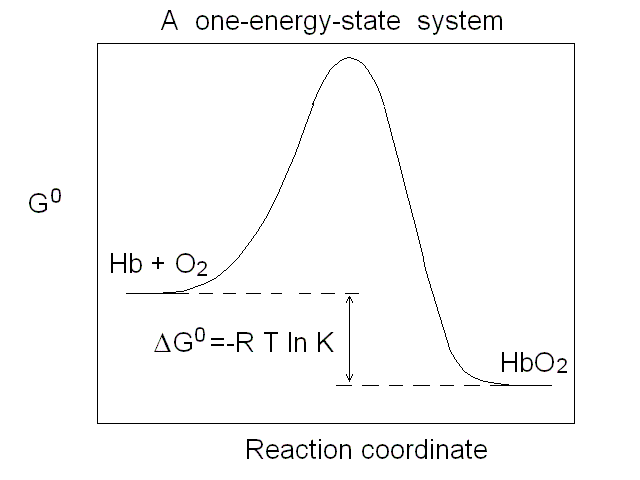
Figure 2. Energy profile of the oxygen binding reaction of a one-state oxygen carrier (corresponds to the dashed line in Figs. 1A, 1B and 1C). An oxygen carrier which can occupy two thermodynamic states has two n=1 asymptotes on the Hill plot, corresponding to two different equilibrium constants and two different ΔG0 values, as depicted in Fig.3. It is important to remark that an oxygen carrier having three or four states may have the same Hill plot as one having only two states, since the mixtures of different states usually do not allow one to resolve more than two n=1 segments. 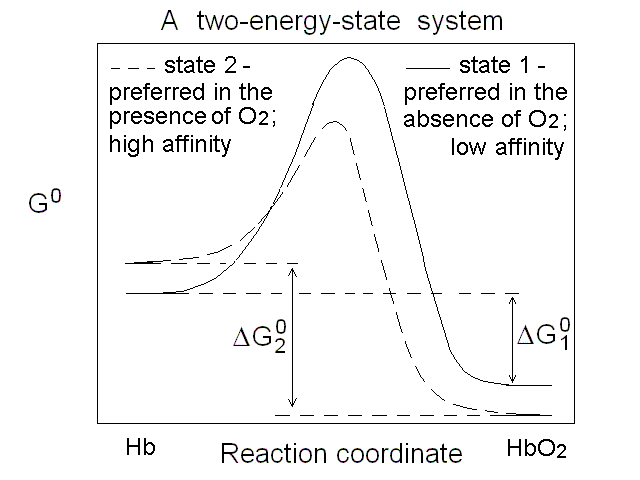
Figure 3. Energy profile of the oxygen binding reactions of a two-state oxygen carrier (corresponds to the continuous line in Figs. 1A, 1B and 1C). Cooperativity is a functional property, but it must have a structural counterpart Cooperativity is the property of a macromolecule whose affinity for its ligands increases as the ligand saturation increases, and as such is a functional concept. However, it has structural implications: we saw that Hill correctly predicted that cooperativity requires a polymeric macromolecule (i.e. more than a single ligand binding site), and reduced population of the ligation intermediates. Adair's four-constants equation did not make any assunmption on the structure of Hb and was thus model-free, but it was only a phenomenological approach and did not in any way explain why the high affinity sites were not present in the unliganded macromolecules. The first attempt to explain cooperativity using a structural model is due to Linus Pauling (whose numerous contributions won him a Nobel Prize for Chemistry in 1954). Paulings model assumed that O2 binding to Hb was associated to the formation of "stabilizing interactions" between subunits, such that the binding of each successive molecule of the gas occurred with an increase in affinity proportional to the number of stabilizing interactions formed in the preceding step. Unfortunately the structure of Hb (determined some 25 years later) did not support Pauling's hypothesis. Which states for human Hb? Under dissociating conditions (e.g. in the presence of urea) or upon separation of the native α and β subunits, the oxygen affinity of Hb increases. Thus the "resting state" of Hb has high O2 affinity. Upon association of the subunits (or the αβ dimers) into unliganded tetramers, the O2 affinity of the macromolecule decreases, demonstrating that the quaternary assembly induces a structural change, however subtle, responsible for "constraining" the affinity. J. Wyman termed this effect the quaternary constraint of hemoglobin. Monod called the high affinity state "relaxed" (or R-state) and the low affinity state "tense" (or T-state). Mims et al. (J. Biol. Chem. 1983, 258, 14219-14232) report the following values for the oxygen affinities of the α and β subunits of human Hb in the two states:
Monod's two-state model: the minimal functioning interpretation of Hb In 1963 Jacques Monod (who won the Nobel Prize for Biology and Medicine in 1965) coined the term "allostery" (literally: other structure) for proteins that, like the Lac repressor of E. coli, are stable in two different structural conformations, each having different functional properties. In 1965 Monod, Wyman and Changeux (MWC) demonstrated that allostery can provide a structural explanation of cooperativity, provided that the cooperative macromolecule were a "symmetric oligomer". The Hb tetramer is symmetric dimer of αβ eterodimers, and was used as an example of the two-state model. The structural implications of the model were obvious but generic, and indeed the structure of Hb was being discovered exactly in th same time. In what follows shall use the MWC model as a reference frame to interpret some key experiments carried out on Hb; further details, as well as the model-free analysis of the same experiments can be found in my paper Bellelli A. (2010) Hemoglobin and Cooperativity: Experiments and Theories. Curr. Protein Pept. Sci. 11: 2-36. The MWC model postulates that Hb is allosteric, i.e. stable in either of two alternative conformations, called R (for relaxed) and T (for tense= constrained) and having different O2 affinity. The structures correspond to energy states and the T-state has lower O2 affinity than the R-state. The T-state/structure is more stable than the R-state in the absence of ligands. These premises dictate the following energy profile for the four-step oxygenation reaction of Hb: 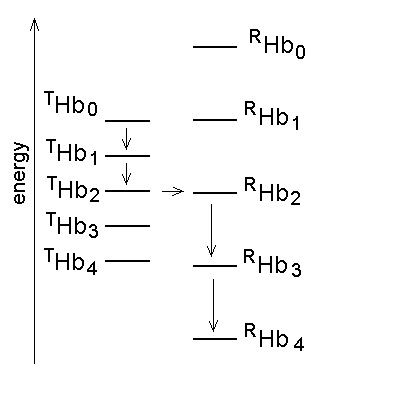
Figure 4. Energy profile of the four-step oxygenation of Hb. T0 indicates unliganded Hb in the T-state (THb); T1 monooxygenated T-state Hb (THbO2); T2 doubly oxygenated T-state Hb (T(HbO2)2); etc. Same for R0 through R4. At each oxygenation step the lower energy state liganded derivative predominates, thus the main path of oxygenation may be indicated as a series of arrows connecting T0 to R4. The T and R states in themselves are non-cooperative: cooperativity arises as a consequence of the oxygen linked structural transition from the T to the R state. The T and R structures coexhist in equilibrium in the presence and in the absence of oxygen and the following relations apply: [THb0] / [RHb0] = L0 [THb1] / [RHb1] = L0 KR / KT = L1 [THbn] / [RHbn] = L0 (KR / KT)n = L1 In the original formulation of the MWC model, here employed, KR and KT were defined as dissociation equilibrium constants, thus KR < KT. Their ratio was called c = KR / KT << 1. For the model to explain cooperativity it is required that L0 >>1 and L4 <<1. The oxygen affinity of Hb in the MWC model is the weighted average of the constant affinities of RHb and RHb; as the oxygena saturation increases the relative population of RHb also increases at the espense of that of THb, and the average oxygen affinity increases. The binding polynomials (= algebraic expressions describing the relative populations of each ligation intermediate) for RHb and THb, using RHb0 as the reference species, are as follows: [RHb]total = [RHb0] (1 + [O2] / KR)4 [THb]total = [RHb0] L0 (1 + [O2] / KT)4 and the complete binding polynomial is: [Hb]total = [RHb0] [(1 + [O2] / KR)4 + L0 (1 + [O2] / KT)4] Structural implications of the MWC model and the actual structure of Hb The main structural requirement of the two-state model is the symmetry of the cooperative macromolecule and the structures of oxy- and deoxy-Hb that Max Perutz (Nobel Prize for Chemistry in 1962) was discovering at the same time by means of X-ray crystallography revealed a high degree of symmetry. The α and β subunits of Hb are small globular hemoproteins made up of eight α-helical segments named A through H. The essential structural difference between their oxygenated and deoxygenated state (aside from the presence of the O2 molecule bound at the heme iron) was observed at the F-helix, whose eight aminoacid residue is a His that is directly coordinated to the heme iron, on the opposite side of O2: 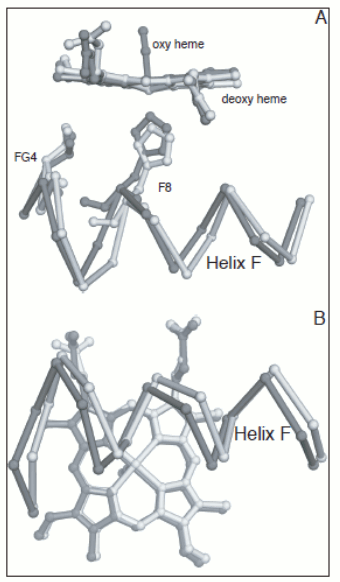
Figure 5. Oxygen-dependent movements of the F helix and the corner between the F and G helices (FG corner) in the α subunit of human Hb. The interfaces between the subunits in Hb are isologous (a term coined by Monod), i.e. the α and β subunits make their contacts using the same structural features. The dimeric α1β1 interface is contributed by helices B, G and H of the partner subunits, with the symmetric contacts α1B - β1H; α1G - β1G; and α1H - β1B. The inter-dimeric α1β2 interface is contributed by helix C and the FG corner of the partner subunits, with the symmetric contacts α1C - β2FG and α1FG - β2C, as shown in the Fig. 6. 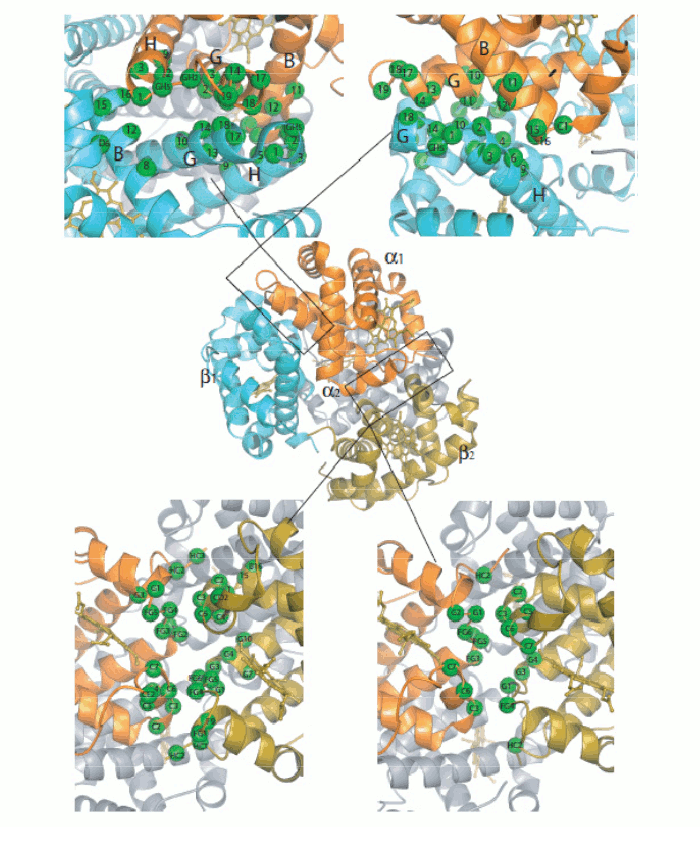
Figure 6. General architecture of the Hb tetramer and enlarged view of the interfaces between the constituent subunits. Perutz's structures seemed to beautifully confirm Monod's hypotheses. e.g. they showed that the oligomer has a (pseudo-)symmetric structure in both allosteric states, and the intersubunit interfaces are isologous and highly symmetric. But why is symmetryb so crucial to allostery and cooperativity? Monod's intuition was that if the oligomer is symmetric and one subunit binds oxygen and undergoes a structural change, then to maintain symmetry the unliganded subunit must also adopt the structural conformation of the liganded one; and thermodynamics dictates that the bound conformation must has affinity. Thus symmetry explains how a liganded subunit may increase the oxygen affinity of a neighbouring unliganded subunit, as in the following example: 
Figure 7. A symmetric homodimer in its unliganded and monoliganded states. Note that to maintain symmetry, the unliganded subunit of the monoliganded homodimer has to adopt the same conformation as the liganded subunit. Note also that the monomers are rotated by 180 degrees with respect to each other and the interface is isologous. Successive structural data, collected over fifty years, povided further support to the MWC model: 1) the structures of the poorly populated state THb4 was solved and good mimics of that of RHb0 are available (e.g. Perutz had solved the structure of BME chemically modified unliganded RHb, and Arnone solved that of the R-state unliganded β4 homotetramer). These confirm that these states exist and that their structure is the same irrespective of ligation, as postulated by the MWC model. 2) Doubly liganded intermediates were mimicked using mixed metal hybrid Hbs. These artificial macromolecules are assembled from native α or β and metal substituted partner subunits. By chosing a suitable metal protoporphyrin IX (eg. Ni, Zn, Mn, or Co) one obtains a five coordinated metal that mimics the unliganded iron but is unable to bind iron ligands (usually CO is used instead of O2). The structures of the diliganded intermediates (αFeCOβNi)2, (αNiβFeCO)2, (αFeCOβCo)2 and (αFeCOβMn)2 have been solved by X-ray crystallography and they invariably correspond to THb: none of these macromolecules has shown an "intermediate" structure. 3) Crystals of THb bind oxygen non-cooperatively and with low affinity, whereas crystals of RHb display lack of cooperativity and high kinetic reactivity. These findings are consistent with the MWC model premise that no cooperativity occurs within each allosteric state, be it R or T. Structure degeneracy of RHb and energy degeneracy of THb Two experimental observations that seem to contrast with the premises of the MWC model: 1) more structures have been reported by X-ray crystallography for the R-state of human (and other) Hb(s). These are called the R, R2, R3 structures. The R-state is thus structurally degenerated. 2) More energy states (i.e. oxygen affinities) have been reported for the T-state of human (and other) Hb(s). The T-state is thus energy degenerated. By contrast structure degeneracy for T-state Hb is very small. In my opinion these discrepancies are only apparent and are easily reconciled with the two-state model. The Structure degeneracy of R-state Hb corresponds to quaternary structures that do not constrain the allosteric interface. M. Brunori and I (BBA 2001, 1807, 1262-1272) measured the distances of selected residues at the cooperative α1β2 interface and could demonstrate that they they neatly cluster in two groups one for the quaternary constrained T-state and one for thye unconstrained R-states: thus the struucture degeneracy of the R-state is perfectly compatiblle with it being a single energy state. This observation is consistent with the espectation that the structural basis of the quaternary constraint is very specific and that any unconstrained structure has the high affinity of the isolated subunits or dimers. Thus only two energy states need to be considered, constrained (T) and unconstrained (R, R2, R3, dimer-lke, isolated subunits-like), as required by the MWC model. 
The energy degeneracy of the T-state was observed (among others) by K. Imai, who showed that the value of KT varies considerably in the presence of allosteric effectors (e.g. hydrogen ions, chloride, DPG, etc.). This was not anticipated by the MWC model, that postulated the allosteric effectors only to bias the allosteric constant L0 (an effector binding preferntially to THb would increase L0, one binding preferentially to RHb would decrease this parameter). Perutz's structures, however, showed that the cooperative α1β2 interface is not the only possible site where constraints can be exerted: further constraints can be exerted to some extent independently of the T and R structures (e.g. at the C-termini of each chain, as demonstrated by experiments in which the C-terminal residue of either or both sununit was cleaved by carboxypeptidase digestion; see Moffat et al. J. Biol. Chem. 1973; 248: 6387-93; Kavanaugh et al., J. Mol. Biol. 1995;248: 136-50). Dissociation into dimers and the MWC model An astonishing success of the MWC model is its ability to describe (perhaps with some approximation) the relationship between oxygenation and dissociation into dimers. It had long been known that liganded Hb easily dissociates into α1β1/type dimers having high oxygen affinity. The KD is in the low micromolar range. Unliganded Hb dissociates some 104 to 105 times less readily. Unliganded dimers have high oxygen affinity, consistent with the quaternary constraints being localized at the α1β2 interface (which is disrupted by dissociation). A scheme of the dimer-tetramer equilibrium, within the framework of the two-state model, and limited to the first oxygenation step is as follows: 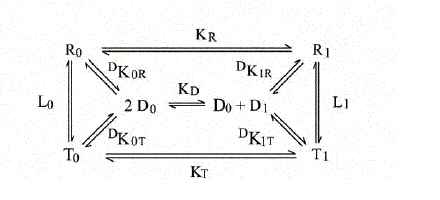
If we consider first the dissociation into dimers for unliganded Hb, we remark that the following relations apply: RHb0 <=> 2 αβ ; DKR,0 = [αβ]2 / [RHb0] THb0 <=> 2 αβ ; DKT,0 = [αβ]2 / [THb0] DKR,0 / DKT,0 = [THb0] / [RHb0] = L0 The MWC model predicts that unliganded T-state Hb is more stable than R-state Hb to dimerization by a factor that equals the allosteric constant L0. We consider next the oxygenation of R-state Hb in relation to its dissociation into dimers. We define: KR = [RHb] [O2] / [RHbO2] KD = [αβ] [O2] / [αβO2] DKR,0 = [αβ]2 / [RHb] DKR,1 = [αβ] [αβO2] / [RHbO2] We remark that: KR DKR,0 = KD DKR,1 Since the αβ dimers have the same O2 affinity as RHb (i.e. KR = KD, it follows that DKR,0 = DKR,1, i.e. in the R-state Hb dimerization is independent of ligation. We finally turn to the oxygenation of T-state Hb in relation to its dissociation into dimers. We define: KT = [THb] [O2] / [THbO2] KD = [αβ] [O2] / [αβO2] DKT,0 = [αβ]2 / [THb] DKT,1 = [αβ] [αβO2] / [THbO2] We remark that: KT DKT,0 = KD DKT,1 Since the αβ dimers have higher O2 affinity than THb (i.e. KT > KD, it follows that DKT,0 < DKT,1, i.e. in the T-state Hb dimerization increases as ligation increases. From the above relations it follows that measurement of the dimer-tetramer equilibrium for different ligation intermediates allows one to reconstruct the whole energy landscape of oxygenation, an approach which was pioneered by Gary K. Ackers (who emphasized some quantitative deviations from the prediction derived from the two-state model). To carry out this type of experiments one needs: 1) to prepare the separated α and β subunits in complex with some slowly dissociating ligand (e.g. the cyano/met derivative or a metal different than iron); 2) to mix each with the partner subunit in the unliganded state; in some cases the tetramer so obtained may need to be mixed with other, differently prepared tetramers and the mixture should be allowed time to equilibrate; 3) to add haptoglobin to the mixture which contains cyano-met/deoxy hybrid tetramers, and to record the time course of dissociation into dimers (by stopped flow); 4) to calculate the equilibrium dimerization constant under the assumption that the combination rate constant of dimers is unchanged and independent of their ligation state. 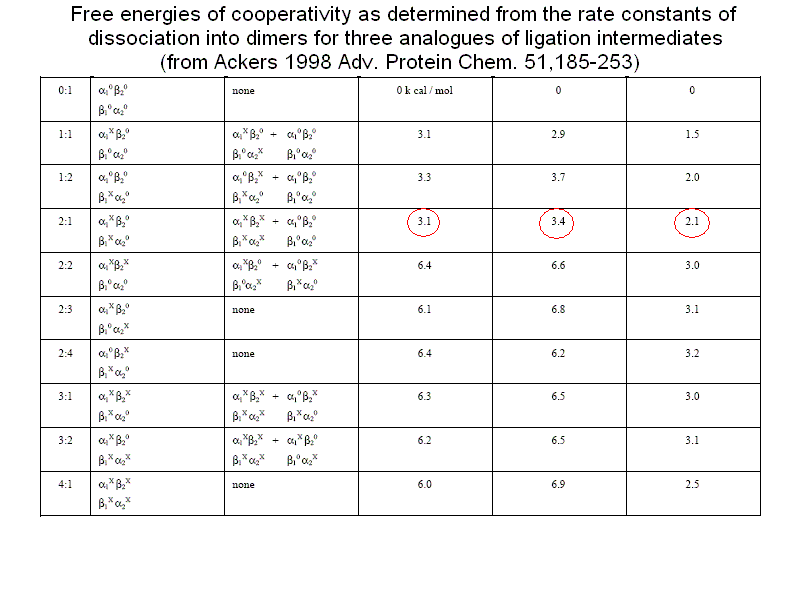
Direct quantitation of ligation intermediates One fundamental tenet of the MWC model is that ligation intermediates adopt either the R or the T conformation and none else; this was addressed with diliganded mixed metal hybrids, as discussed above. However, experiments on metal hybrids cannot give information about the relative concentration of the different intermediate, which, as recognized already by Hill, is at the very basis of cooperativity. In a cooperative oxygen carrier ligation intermediates attain very low concentration and are difficult to measure and characterize. M. Perrella devised and experimental method to determine the relative concentrations of ligation intermediates: 1) he anaerobically mixed Hb and HbCO in the desired proportions and allowed the mixture to reach its equilibrium conditions; 2) then he mixed the Hb solution with a ferricyanide solution at -30 C. Under these exoperimental conditions the unliganded heme iron is rapidly oxidized to the ferric state, whereas the CO-bound iron remains reduced. 3) Finally he separated the components of the ferric / ferrous-CO derivatives by means of low temperature isoelectric focusing, taking advantage of the different charges due to the iron oxidation state and to the protonation state of the subunits. Figure 8 reports two such experiments, together with their densitograms: 
Figure 8. Two isoelectrofocusing runs of the ligation intermediates of HbCO, with the pertinent electroferograms. The identification of the bands 1-9 is as from the following table: 
How do Perrella's measurments of ligation intermediate concentrations correlate with the predictions of the MWC model? The first observation is that the MWC model assumes perfect symmetry, and this implies statistical population of equally liganded intermediates (e.g. [ααCOβ2] = [α2ββCO]). This is not usually the case in these measurements, but one should take into account the small difference in oxygen affinity of the two subunits (that the model ignores). Indeed the MWC model only allows one to calculate the sum of equally liganded intermediates, with the formula that one may derive from the binding polynomial:
An example of Perrella's results is reported in the following table, which shows that the main discrepancy between data and predictions is in the concentration of the doubly liganded intermediates: 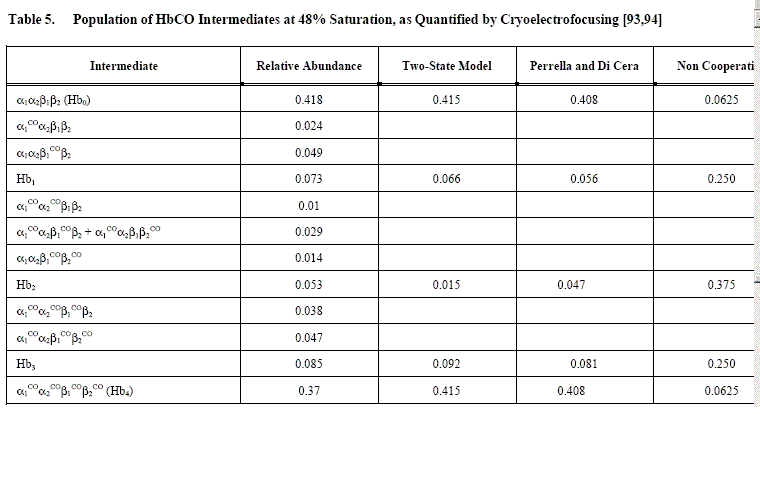
Home page |